15. Polar Coordinates
e. Arc Length of a Polar Graph
In the chapter on Arc Length, we learned that the arc length of a parametric curve, \(\vec{r}(t)=(x(t),y(t))\), from \(t=a\) to \(t=b\) is: \[ L=\int_a^b \sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt \] We also know that any polar curve, \(r=r(\theta)\), can be regarded as the parametric curve \[ \vec{r}(\theta)=(x(\theta),y(\theta)) =(r(\theta)\cos\theta,r(\theta)\sin\theta) \] where the parameter \(t\) has been replaced by a parameter \(\theta\).
\(\vec r(\theta)\) is the position vector (Notice the arrow over the \(\vec r\).) telling us the position in the plane for each value of the parameter \(\theta\), whereas \(r(\theta)\) is simply the function defining the polar curve. Don't get confused.
Consequently:
The arc length of a polar curve, \(r=r(\theta)\), from \(\theta=\alpha\) to \(\theta=\beta\) is \[ L=\int_\alpha^\beta \sqrt{\,r(\theta)^2+\left(\dfrac{dr}{d\theta}\right)^2}\,d\theta \]
In the arc length formula, we need to replace \(t\) by \(\theta\), \(a\) by \(\alpha\) and \(b\) by \(\beta\): \[ L=\int_\alpha^\beta \sqrt{\left(\dfrac{dx}{d\theta}\right)^2 +\left(\dfrac{dy}{d\theta}\right)^2}\,d\theta \] Then we simply need to transform the quantity inside the square root: \[\begin{aligned} \left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta }\right)^2 &=(r'\cos\theta-r\sin\theta)^2 +(r'\sin\theta+r\cos\theta)^2 \\ &=(r')^2\cos^2\theta-2r' r\sin\theta\cos\theta+r^2\sin^2\theta \\ &\quad+(r')^2\sin^2\theta+2r' r\sin\theta\cos\theta+r^2\cos^2\theta \\ &=(r')^2+r^2 \end{aligned}\]
Find the arc length of the cardioid, \(r=1+\cos\theta\).
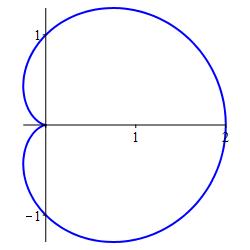
You may have noticed that the cardioids have been especially easy to work with. Here, however, we encounter some complications. We first set up the integral: Since \(r=1+\cos\theta\) we have \(\dfrac{dr}{d\theta}=-\sin\theta\). Since the cardioid is swept out once between \(\theta=0\) and \(\theta=2\pi\), the arc length is: \[\begin{aligned} L &=\int_0^{2\pi} \sqrt{(1+\cos\theta)^2+\sin^2\theta }\,d\theta \\ &=\int_0^{2\pi} \sqrt{1+2\cos\theta+\cos^2\theta+\sin^2\theta}\,d\theta \\ &=\int_0^{2\pi} \sqrt{2+2\cos\theta}\,d\theta =\sqrt{2}\int_0^{2\pi} \sqrt{1+\cos\theta}\,d\theta \end{aligned}\] As with all arclength problems, there is some trick which allows us to compute the integral.
One trick is to multiply by \(\dfrac{\sqrt{1-\cos\theta}}{\sqrt{1-\cos\theta}}\) \[\begin{aligned} L &=\sqrt{2}\int_0^{2\pi} \sqrt{1+\cos\theta} \dfrac{\sqrt{1-\cos\theta}}{\sqrt{1-\cos\theta}}\,d\theta \\ &=\sqrt{2}\int_0^{2\pi} \dfrac{\sqrt{1-\cos^2\theta}}{\sqrt{1-\cos\theta}}\,d\theta =\sqrt{2}\int_0^{2\pi} \dfrac{\sqrt{\sin^2\theta}}{\sqrt{1-\cos\theta}}\,d\theta \end{aligned}\] We now hit a second problem: \(\sqrt{\sin^2\theta}=|\sin\theta|\), not \(\sin\theta\). So either we need to split up the integral according to whether \(\sin\theta \gt 0\) or \(\sin\theta \lt 0\) or we need to take advantage of the symmetry of the cardioid by finding the length of half the cardioid and doubling it. We do the latter: The upper half of the cardioid corresponds to \(0 \le \theta \le \pi\). On this interval, \(\sin\theta \ge 0\), so that \(\sqrt{\sin^2\theta}=\sin\theta\). Consequently, the arc length is: \[ L=2\sqrt{2}\int_0^\pi \dfrac{\sin\theta}{\sqrt{1-\cos\theta}}\,d\theta \] Now we can integrate by making the substitution \(u=1-\cos\theta\), so that \(du=\sin\theta\,d\theta\). Consequently; \[\begin{aligned} L &=2\sqrt{2}\int_0^2 \dfrac{du}{\sqrt{u}} =2\sqrt{2}\left[2u^{1/2}\rule{0pt}{10pt}\right]_0^2 \\ &=2\sqrt{2}\left[2\sqrt{2}\right]=8 \end{aligned}\]
A second trick is to apply the identity \(\cos^2A=\dfrac{1+\cos(2A)}{2}\) with \(A=\dfrac{\theta}{2}\). Then \(2\cos^2\dfrac{\theta}{2}=1+\cos\theta\). So: \[\begin{aligned} L&=\sqrt{2}\int_0^{2\pi} \sqrt{1+\cos\theta}\,d\theta =\sqrt{2}\int_0^{2\pi} \sqrt{2\cos^2\dfrac{\theta}{2}}\,d\theta \\ &=2\int_0^{2\pi} \sqrt{\cos^2\dfrac{\theta}{2}}\,d\theta \end{aligned}\] Again we need to compute the arclength for half of the curve and double it. For \(0 \le \theta \le \pi\), we have \(0 \le \dfrac{\theta}{2} \le \dfrac{\pi}{2}\), and \(\cos\dfrac{\theta}{2} \ge 0\). So \(\sqrt{\cos^2\dfrac{\theta}{2}}=\cos\dfrac{\theta}{2}\). Consequently, the arc length is: \[ L=4\int_0^\pi \cos\dfrac{\theta}{2}\,d\theta =4\left[2\sin\dfrac{\theta}{2}\right]_0^\pi =8\sin\dfrac{\pi}{2}=8 \]
Find the arc length of the circle given by the polar equation, \(r=\sin\theta\).
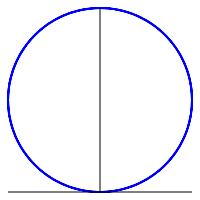
The curve is a circle. It is traced twice as \(\theta\) increases from \(0\) to \(2\pi\). So you only need to integrate for \(0 \le \theta \le \pi\).
\(L=\pi\)
The circle is traced twice as \(\theta\) increases from \(0\) to \(2\pi\). So we only need to integrate for \(0 \le \theta \le \pi\). Since \(r(\theta)=\sin\theta\), we have \(r'(\theta)=\cos\theta\) and: \[ L=\int_0^\pi \sqrt{\sin^2\theta+\cos^2\theta}\,d\theta =\int_0^\pi 1\,d\theta=\left.\theta\rule{0pt}{10pt}\right|_0^\pi=\pi \]
You should know the answer since the graph is a circle with radius \(\dfrac{1}{2}\). So its length (circumference) is: \[ C=2\pi r=2\pi(1/2)=\pi \]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum